Алгоритм кластеризации
ISODATA (ИСОМАД)Алгоритм кластеризации
ISODATA(ИСОМАД) предназначен для разделения заданного множества образов (в данном случае точек двумерного пространства) на подмножества (кластеры), связанные определенным свойством, например основанное на близости точек по геометрическому расстоянию. Алгоритм эвристический, т.е. результат работы во многом зависит от заданных начальных параметров.При работе с набором
{x1, x2, ..., xN}, составленным из N элементов, алгоритм ИСОМАД выполняет следующие основные шаги.Шаг
1. Задаются параметры, определяющие процесс кластеризации:К
QN —параметр, с которым сравнивается количество выборочных образов, вошедших в кластер;
Qs— параметр, характеризующий среднеквадратичное отклонение;
Qc—параметр, характеризующий компактность;
L— максимальное количество пар центров кластеров, которые можно объединить;
I — допустимое число циклов итерации.
Шаг 2. Заданные N образов распределяются по кластерам, соответствующим выбранным исходным центрам, по правилу
xÎ Sj,
если ||х – zj|| < ||х – zi||, i=1,2, ..., Nc; i¹ j,применяемому ко всем образам х, вошедшим в выборку; через
Sj обозначено подмножество образов выборки, включенных в кластер с центром zj.Шаг
3. Ликвидируются подмножества образов, в состав которых входит менее QN элементов, т. е. если для некоторого j выполняется условие Nj < QN, то подмножество Sj исключается из рассмотрения и значение Nc уменьшается на 1.Шаг
4. Каждый центр кластера zj, j=1, 2, ..., Nc, локализуется и корректируется посредством приравнивания его выборочному среднему, найденному по соответствующему подмножеству Sj, т. е.![]()
где
Nj —число объектов, вошедших в подмножество Nj.Шаг
5. Вычисляется среднее расстояние Dj между объектами, входящими в подмножество Sj, и соответствующим центром кластера по формуле![]()
Шаг
6. Вычисляется обобщенное среднее расстояние между объектами, находящимися в отдельных кластерах, и соответствующими центрами кластеров по формуле![]()
Шаг
7. (а) Если текущий цикл итерации—последний, то задается Qc=0; переход к шагу 11. (б) Если условие Nc<=К/2 выполняется, то переход к шагу 8. (в) Если текущий цикл итерации имеет четный порядковый номер или выполняется условие Nc>=K/2, то переход к шагу 11; в противном случае процесс итерации продолжается.Шаг
8. Для каждого подмножества выборочных образов с помощью соотношения![]()
вычисляется вектор среднеквадратичного отклонения
s j = (s 1j, s 2j, ..., s nj)', где п есть размерность образа, xik, есть i-я компонента k-ro объекта в подмножестве Sj, zij есть i-я компонента вектора, представляющего центр кластера zj, и Nj —количество выборочных образов, включенных в подмножество Sc. Каждая компонента вектора среднеквадратичного отклонения s j характеризует среднеквадратичное отклонение образа, входящего в подмножество Sj, по одной из главных осей координат.Шаг
9. В каждом векторе среднеквадратичного отклонения s j, j=1, 2, ..., Nc, отыскивается максимальная компонента s jmax.Шаг
10. Если для любого s jmax, j=1, 2, ..., Nc, выполняются условия s jmax>Qs,иа
)или
б) Nj < К/2,
то кластер с центром zj расщепляется на два новых кластера с центрами zj+ и zj- соответственно, кластер с центром zj ликвидируется, а значение Nc увеличивается на 1. Для определения центра кластера zj+ к компоненте вектора zj, соответствующей максимальной компоненте вектора s j, прибавляется заданная величина g j; центр кластера zj- определяется вычитанием этой же величины g j из той же самой компоненты вектора zj. В качестве величины g j можно выбрать некоторую долю значения максимальной среднеквадратичной компоненты s jmax, т. е. положить g j = ks jmax, где 0 < k <= 1. При выборе g j следуег руководствоваться в основном тем, чтобы ее величина была достаточно большой для различения разницы в расстояниях от произвольного образа до новых двух центров кластеров, но достаточно малой, чтобы общая структура кластеризации существенно не изменилась.
Если расщепление происходит на этом шаге, надо перейти к шагу 2, в противном случае продолжать выполнение алгоритма.
Шаг 11. Вычисляются расстояния Dij между всеми парами центров кластеров:
Dij
=l| zi - zj ||, i=1, 2, ..., Nc-1; j=i+1, 2, ..., Nc.Шаг
12. Расстояния Dij сравниваются с параметром Qc. Те L расстояний, которые оказались меньше Qc, ранжируются в порядке возрастания:[Di1j1, Di2j2, ..., DiLjL,]
причем
Di1j1 < Di2j2 < ... < DiLjL,. a L—максимальное число пар центров кластеров, которые можно объединить. Следующий шаг осуществляет процесс слияния кластеров.Шаг
13. Каждое расстояние Diljl вычислено для определенной пары кластеров с центрами zil и zjl. К этим парам в последовательности, соответствующей увеличению расстояния между центрами, применяется процедура слияния, осуществляемая на основе следующего правила.Кластеры с центрами
zil и zjl, i=1, 2, ..., L, объединяются (при условии, что в текущем цикле итерации процедура слияния не применялась ни к тому, ни к другому кластеру), причем новый центр кластера определяется по формуле![]()
Центры кластеров
zil и zjl ликвидируются и значение Nc уменьшается на 1.Отметим, что допускается только попарное слияние кластеров и центр полученного в результате кластера рассчитывается, исходя из позиций, занимаемых центрами объединяемых кластеров и взятых с весами, определяемыми количеством выборочных образов в соответствующем кластере. Опыт свидетельствует о том, что использование более сложных процедур объединения кластеров может привести к получению неудовлетворительныхрезультатов. Описанная процедура обеспечивает выбор в качестве центра объединенного кластера точки, представляющей истинное среднее сливаемых подмножеств образов. Важно также иметь в виду, что, поскольку к каждому центру кластера
процедуру слияния можно применить только один раз, реализация данного шага ни при каких обстоятельствах не может привести к получению L объединенных кластеров.Шаг 14. Если текущий цикл итерации—последний, то выполнение алгоритма прекращается. В противном случае следует возвратиться либо к шагу 1, если по предписанию пользователя меняется какой-либо из параметров, определяющих процесс кластеризации, либо к шагу 2, если в очередном цикле итерации параметры процесса должны остаться неизменными. Завершением цикла итерации считается каждый переход к шагам I или 2.
Пример.
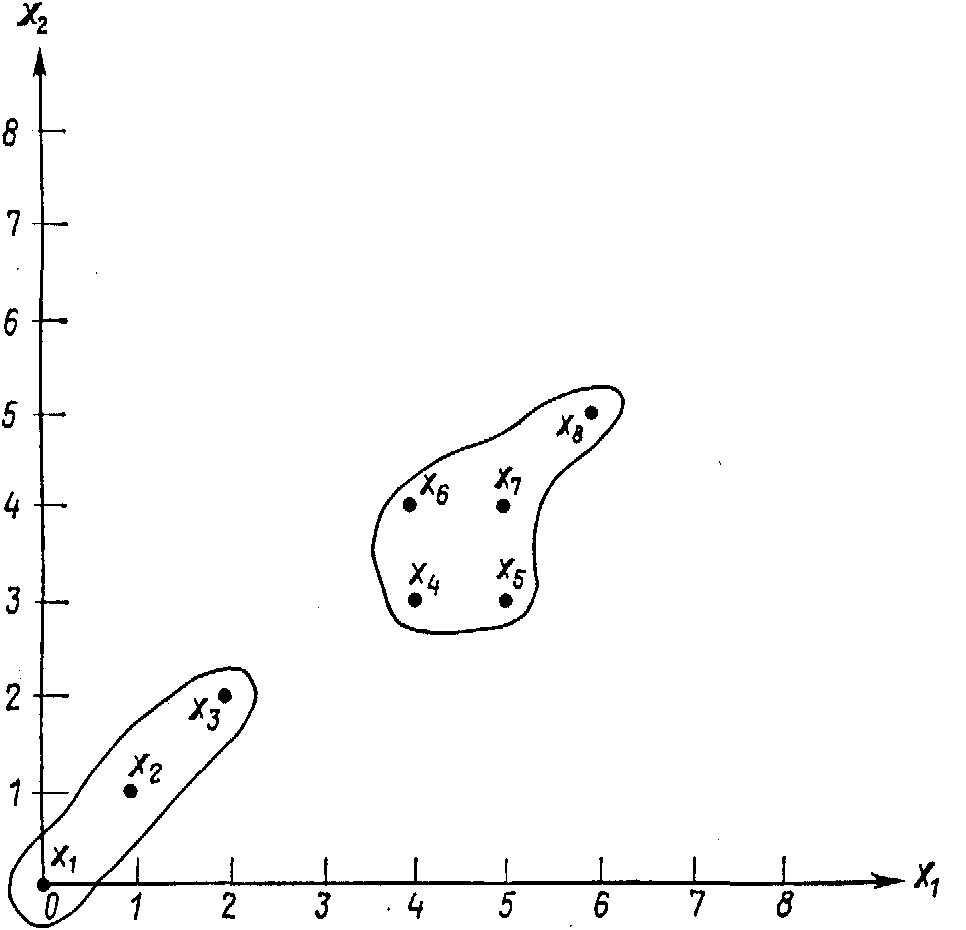
Выборка образов, использованная для иллюстрации работы алгоритма ИСОМАД.
Хотя алгоритм ИСОМАД не очень подходит для ручных вычислений, принцип его работы можно проиллюстрировать на простом примере. Рассмотрим выборку, образы которой размещены так, как это изображено на рис. 3.11.
В данном случае
N ==8 и п = 2. В качестве начальных условий задаем Nc=1, z1 = (0,0)' и следующие значения параметров процесса кластеризации:Шаг 1.
К=2,
QN=1, Qs=1, Qc=4, L=0, I=4.Если всякая априорная информация об анализируемых данных отсутствует, эти параметры выбираются произвольным образом и затем корректируются от итерации к итерации.
Шаг 2. Так как задан только один центр кластера, то
S1 ={x1, x2, ..., x8} и N1 = 8.
Шаг 3.
Поскольку N1 > QN, ни одно подмножество не ликвидируется.Шаг
4. Корректируется положение центра кластера:![]()
Шаг 5.
Вычисляется расстояние Dj:![]()
Шаг 6.
Вычисляется расстояние D:D = D1 = 2,26.
Шаг 7.
Поскольку данный цикл итерации—не последний и Nc = К/2, осуществляется переход к шагу 8.Шаг 8. Для подмножества S1 вычисляется вектор среднеквадратичного отклонения:
![]()
Шаг 9.
Максимальная компонента вектора s 1 равна 1,99, следовательно, s 1max = 1,99.Шаг 10.
Поскольку s 1max > Qs, и Nc = К/2, кластер с центром z1 расщепляется на два новых кластера. Следуя процедуре, предусмотренной шагом 10, выбираем g j = 0,5s jmax = 1,0. При этом![]()
Для удобства записи будем называть центры этих кластеров
z1 и z2 соответственно. Значение Nc увеличивается на 1; переход к шагу 2.Шаг 2. Подмножества образов имеют теперь следующий вид:
S1 ={x4, x5, ..., x8}, S2 ={x1, x2, x3} и N1 = 5, N2 = 3.
Шаг 3.
Поскольку обе величины—и N1, и N2—больше QN, ни одно подмножество не ликвидируется.Шаг 4. Корректируется положение центров кластеров:
![]()
Шаг 5.
Вычисляется расстояние Dj, j=1,2: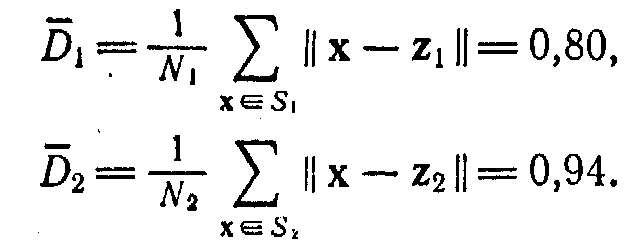
Шаг 6.
Вычисляется расстояние D:
Шаг 7.
Поскольку данная итерация имеет четный порядковый номер, условие (в) шага 7 выполняется. Поэтому следует перейти к шагу 11.Шаг 11.
Вычисление расстояний между парами центров кластеров:![]()
Шаг 12.
Величина расстояния D12 сопоставляется с параметром Qc. В данном случае D12 > Qc.Шаг 13.
Результаты шага 12 показывают, что объединение кластеров невозможно.Шаг 14. Поскольку данный цикл итерации—не последний, необходимо принять решение: вносить или не вносить изменения в параметры процесса кластеризации. Так как в данном (простом) случае 1) число выделенных кластеров соответствует заданному, 2) расстояние между ними больше среднего разброса, характеризуемого среднеквадратичными отклонениями, и 3) каждый кластер содержит существенную часть общего количества выборочных образов, то делается вывод о том, что локализация центров кластеров правильно отражает специфику анализируемых данных. Следовательно, переходим к шагу 2.
Шаги 2—6 дают те же результаты, что и в предыдущем^ цикле итерации.
Шаг 7. Ни одно из условий, проверяемых при реализации данного шага, не выполняется. Поэтому переходим к шагу 8.
Шаг 8. Для множеств S1 ={x4, x5, ..., x8}, S2 ={x1, x2, x3}
![]()
Шаг 9.
В данном случае s 1max = 0,75 и s 2max = 0,82.Шаг 10.
Условия расщепления кластеров не выполняются. Следовательно, переходим к шагу 11. .Шаг 11.
Полученный результат идентичен результату последнего цикла итерации![]()
Шаг 12.
Полученный результат идентичен результату последнего цикла итерации.Шаг 13. Полученный результат идентичен результату последнего цикла итерации.
Шаг 14. На данном цикле итерации не были получены новые-результаты, за исключением изменения векторов среднеквадратичного отклонения. Поэтому переходим к шагу 2.
Шаги 2—6
дают те же результаты, что и в предыдущем;цикле итерации.
Шаг 7. Поскольку данный цикл итерации—последний, задаем Qc = 0 и переходим к шагу 11.
Шаг 11. Как и раньше,
![]()
Шаг 12.
Полученный результат идентичен результату последнего цикла итерации.Шаг 13. Результаты шага 12 показывают, что объединение кластеров невозможно.
Шаг 14. Поскольку данный цикл итерации—последний, выполнение алгоритма заканчивается.
Даже из этого простого примера должно быть ясно, что применение алгоритма ИСОМАД к набору данных умеренной сложности в принципе позволяет получить интересные результаты только после проведения обширных экспериментов. Выявление структуры данных может быть, однако, существенно ускорено благодаря эффективному использованию информации, получаемой после каждого цикла итерационного процесса. Эту информацию, как будет показано ниже, можно использовать для коррекции параметров процесса кластеризации непосредственно при реализации алгоритма.
Используемая литература
:Ту Дж.
, Гонсалес Р. “Принципы распознавания образов” Мир:1978г.